As promised from the last blog, I’ll be going over the the other two common ways for implementing a DFS traversal on a binary tree. The names of the techniques are pre-order and post-order.
Some refreshers
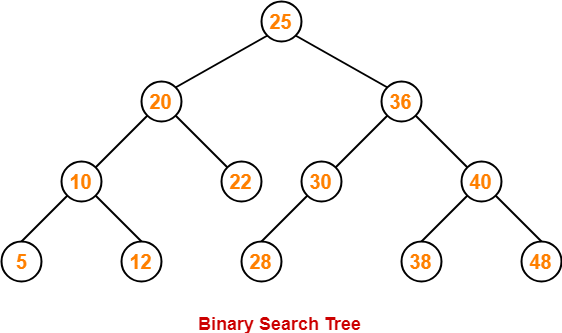
Remember that a binary tree is typically structured with nodes and children nodes. There are a plethora of ways to traverse through a binary tree which include BFS which starts at the top of the tree and proceeding down or DFS which starts from the bottom going up. We covered how to recursively implement a in-order search which as the name states will print or console log the nodes in order. Here was the sample code from the last blog post.


The Pre-order traversal (Root-Left-Right)
The pre-order traversal essentially starts from the parent node, prints it, then proceeds to go down the left side printing the values, and then to the right side recursively. Below is a gif that can help you visualize what’s happening.

As you can see from the gif, we start at the root of 4, print it, head down to the left, print the value, and continue until we can no longer go further left. Then we visit the right side to do the same as the left. Check out the javascript snippet below to see what an implementation looks like.

The post-order traversal (Left-Right-Root)
With this method of traversal, we’ll be recursively going down the left subtrees, printing the value/node once it reaches the bottom, then doing the same for the right side, and the going back up. Take a look at the gif example below to see it visually.

As you can see, we visit the deepest node on the left, print it, then visit the right leaf of the left subtree, print it, and then go up to print the parent root. This is done recursively starting from the the left side, and then eventually executed on the right side of the binary tree. As usual I’ve included a javascript snippet for you to see below.

You can see that the in-order, pre-order, and post-order are very similar but the difference is the ordering of when/where to print or console log the root. By shifting it around, you can implement different traversal methods depending on your use case or requirements. So why are these useful traversals useful? Well, through a combination of these traversals, you can essentially create a binary search tree! I won’t go into too much detail because a binary tree and a binary search tree are not the same. Next time we’ll visit the BFS traversal now that the common DFS traversals are covered. Hopefully you’ve found this blog helpful!