Binary tree-DFS traversals,-in-order

Hi everyone, today we’ll be briefly going over the data structure of binary trees and taking a quick look at different ways to traverse them. Given that these are common interview questions, I would highly recommend to first get familiar with what they are (visually and why they’re important) along with understanding Big-O notations. I’ll be making a series of these traversals with the first blog on in-order traversals, followed by pre-order, and post-order.

What’s the inspiration?

Having recently completing an interview, I was given a binary tree in-order traversal problem. As mentioned, my knowledge was only surface level and there were definitely more that I wished I knew. So afterwards I started digging a bit more to have a better grasp of this particular data structure and the algorithms in case it shows up again!

Some Theory Review

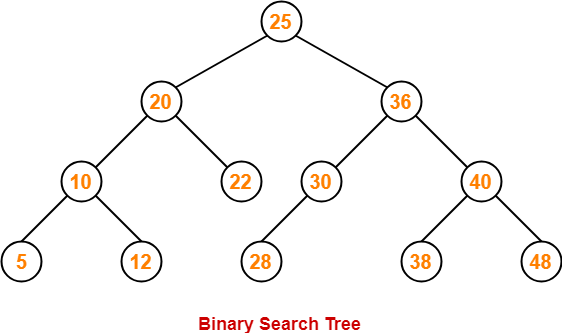
There are primarily 2 types of searches that are most common, Breadth-First-Search(BFS) or Depth-First-Search(DFS), though there are more that can be discussed later. Binary trees are data structures that follow the convention of having a ‘node’ and children nodes. Take a look at the example picture underneath to help you visualize.

Binary Tree Data Structure Example

DFS Traversals

It’s super easy to be overloaded with a bunch of information, so I’ll focus on DFS searches in this blog. If you’re interested in the other types, please feel free to look them up as well. With the category of DFS, there are what’s known as In-order, Pre-order, and Post-order traversals. These all aim to first go to the deepest node of the tree, then going backup once it can’t go any farther down, and to explore what paths are available from there. Take note that in binary trees, it typically goes left to right meaning it’ll evaluate the left side first, then head over to the right side to do the same evaluation.

In-order Traversals (Left-Root-Right)

Here are some key aspects of the the In-order traversal. It will produce a list of the nodes in a sorted order because the value of the left subtrees contains smaller numbers and the right subtree values will contain larger numbers. Take a look at the example below to get a better idea!

In-order search courtesy of giphy

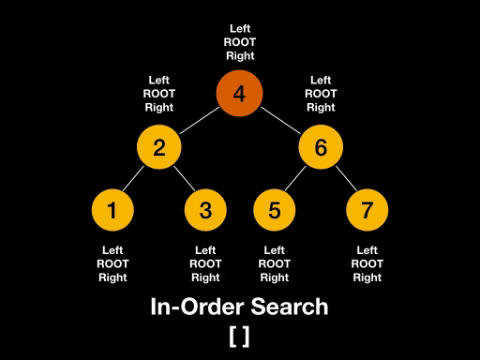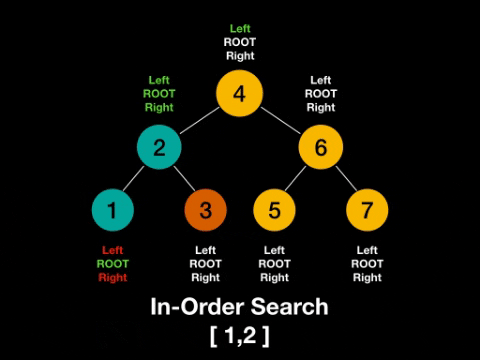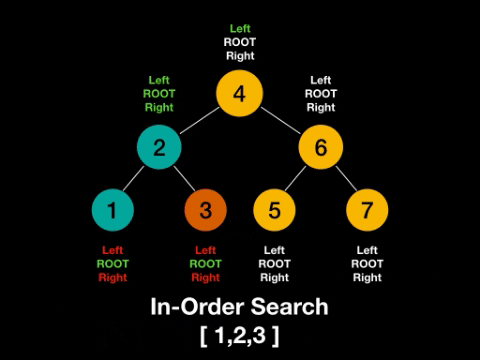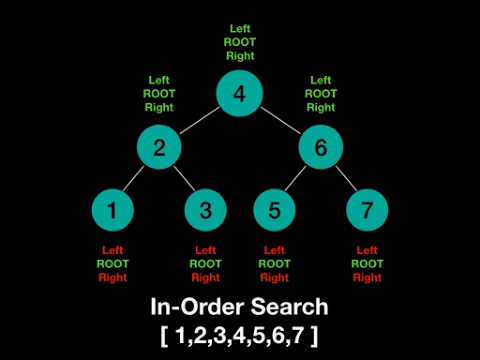
Let’s discuss the “trick” or formula

When given a task to print the task to print the nodes in order, we’d want to create a function that does a few things recursively.

1. Let’s check if the the root node is valid (there is a left child node starting from the current node).
2. Let’s dive into the left subtree all the way down recursively.
3. Let’s print the node and start heading back up to rinse and repeat.
4. Let’s go do the same on the right side for steps 1–3.

Below is a code snippet in Javascript to help visualize what the function would semi look like.

JS code for Snippet In-Order search

Hope all that reads this will find the blog helpful and stay tuned for the next one which I’ll be covering the pre-order search method of Binary Trees.